Weighty matter

Springboarding off yesterday's post, about a discovery of fossils that seem to have come from animals killed the day the Chicxulub Meteorite struck 66 million years ago, today we have a paper in arXiv that looks at why the meteorite hit in the first place.

When you're talking about an event that colossal, I suppose it's natural enough to cast about for a reason other than just shrugging and saying, "Shit happens."  But even allowing for that tendency, the solution landed upon by Leandros Perivolaropoulos, physicist at the University of Ioannina (Greece), seems pretty out there.

Perivolaropoulos attributes the meteorite strike to a sudden increase in Newton's gravitational constant, G -- the number that relates the ratio of the product of two masses and the square of the distance between them to the magnitude of the gravitational force:

The generally accepted value for G is 6.67430 x 10^-11 m^3 kg^-1 s^-2.  Being a constant, the assumption is that it's... constant.  And always has been.

Perivolaropoulos's hypothesis is that millions of years ago, there was a sudden jump in the value of G by about ten percent.  As you can tell from the above equation, if you keep the masses and the distance between them constant, F is directly proportional to G; if G increased by ten percent, so would the magnitude of the gravitational force.  His thought is that this spike in the attractive force caused the orbits of asteroids and comets to destabilize, and sent them hurtling in toward the inner Solar System.  The result: collisions that marked the violent, sudden end of the Mesozoic Era and the hegemony of the dinosaurs.

To be fair to Perivolaropoulos, his surmise is not just based on a single meteorite collision.  He claims that this increase in G could also resolve the "Hubble crisis" -- the fact that two different measures of the rate of the expansion of the universe generate different answers.  The first, using the cosmic microwave background radiation, comes up with a value of 67.8 kilometers/second/megaparsec; the second, from using "standard candles" like Cepheid variables and type 1A supernovas, comes up with 73.2.  (You can read an excellent summary of the dispute, and the current state of the research, here.)

[Image is in the Public Domain courtesy of NASA]

Perivolaropoulos says that his hypothesis takes care of both the Hubble crisis and the reason behind the end-Cretaceous meteorite collision in one fell swoop.

Okay, where to start?

There are a number of problems with this conjecture.  First -- what on earth (or off it) could cause a universe-wide alteration in one of the most fundamental physical constants?  Perivolaropoulos writes, "Physical mechanisms that could induce an ultra-late gravitational transition include a first order scalar tensor theory phase transition from an early false vacuum corresponding to the measured value of the cosmological constant to a new vacuum with lower or zero vacuum energy."  Put more simply, we're looking at a sudden phase shift in space/time, analogous to what happens when the temperature of water falls below 0 C and it suddenly begins to crystallize into ice.  But why?  What triggered it?

Second, if G did suddenly increase by ten percent, it would create some serious havoc in everything undergoing any sort of gravitational interaction.  I.e., everything.  Just to mention one example, the relationship between the mass of the Sun, the velocity of a planet, and the distance between the two is governed by the equation

 

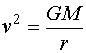
So if the Earth (for example) experienced a sudden increase in the value of G, the radius of its orbit would (equally suddenly) decrease by ten percent.  Moving the Earth ten percent closer to the Sun would, of course, lead to an increase in temperature.  Oh, he says, but that actually happened; ten million years after the extinction of the dinosaurs we have the Paleocene-Eocene Thermal Maximum, when the temperatures went up by something like 7 C.  However, the PETM is sufficiently explained by a fast injection of five thousand gigatons of carbon dioxide into the atmosphere and oceans, likely triggered by massive volcanism in the North Atlantic Igneous Province -- and there's significant evidence of a carbon dioxide spike from stratigraphic evidence.  No need for the Earth to suddenly lurch closer to the Sun.

It wouldn't just affect orbits, of course.  Everything would suddenly weigh ten percent more.  It would take more energy to run, jump, even stand up.  Mountain building would slow down.  Anything in freefall -- from boulders in an avalanche to raindrops -- would accelerate faster.  Tidal fluctuations would decrease (although with the Moon now closer to the Earth, maybe that one would balance out).  

Also, if G did increase everywhere -- it's called the "universal gravitational constant," after all -- then the same thing would have happened simultaneously across the entire universe.  Then, for some reason, there was a commensurate decrease sometime between then and now, leveling G out at the value we now measure.  So we really need not one, but two, mysterious unexplained universal phase transitions, as if one weren't bad enough.

Then there's the issue that the discrepancy in the measurement in the Hubble constant isn't as big as all that -- it's only 3.4 sigma, not yet reaching the 5 sigma threshold that is the touchstone for results to be considered significant in (for example) particle physics.  Admittedly, 3.4 sigma isn't something we can simply ignore; it definitely deserves further research, and (hopefully) an explanation.  But explaining the Hubble constant measurement issue by appeal to an entirely different set of discrepant measurements that have way less experimental support seems like it's not solving anything, it's just moving the mystery onto even shakier ground.

Last, though, I come back to two of the fundamental rules of thumb in science; Ockham's razor (the explanation that adequately accounts for all the facts, and requires the fewest ad hoc assumptions, is most likely to be correct) and the ECREE principle (extraordinary claims require extraordinary evidence).  Perivolaropoulos's hypothesis not only blasts both of those to smithereens, it postulates a phenomenon that occurred once, millions of years ago, then mysteriously reversed itself, and along the way left behind no other significant evidence.

I hate to break out Wolfgang Pauli's acerbic quote again, but "This isn't even wrong."

Now, to be up front, I'm not a physicist.  I have a distantly-remembered B.S. in physics, which hardly qualifies me to evaluate an academic paper on the subject with anything like real rigor.  So if there are any physicists in the studio audience who disagree with my conclusions and want to weigh in, I'm happy to listen.  Maybe there's something going on here that favors Perivolaropoulos's hypothesis that I'm not seeing, and if so, I'll revise my understanding accordingly.

But until then, I think we have to mark the Hubble crisis as "unresolved" and the extinction of the dinosaurs as "really bad luck."

**************************************

A window on the deep past

When I was a kid, I always enjoyed going on walks with my dad.  My dad wasn't very well educated -- barely finished high school -- but was incredibly wise and had an amazing amount of solid, practical common sense.  His attitude was that God gave us reasoning ability and we had damn well better use it -- that most of the questions you run into can be solved if you just get your opinions and ego out of the way and look at them logically.

The result was that despite never having had a physics class in his life, he was brilliant at figuring things out about how the world works.  Like the mind-blowing (well, to ten-year-old kid, at least) idea he told me about because we saw a guy pounding in a fence post with a sledgehammer.

The guy was down the street from us -- maybe a hundred meters away or so -- and I noticed something weird.  The reverberating bang of the head of the sledge hitting the top of the post was out of sync with what we were seeing.  We'd see the sledge hit the post, then a moment later, bang.

I asked my dad about that.  He thought for a moment, and said, "Well, it's because it takes time for the sound to arrive.  The sound is slower than light is, so you see the hammer hit before you hear it."  He told me about how his father had taught him tell how close a thunderstorm is by counting the seconds between the lightning flash and the thunderclap, and that the time got shorter the closer it was.  He pointed at the guy pounding in the fence post, and said, "So the closer we get to him, the shorter the delay should be between seeing the hammer hit and hearing it."

Which, of course, turned out to be true.

But then, a crazy thought occurred to me.  "So... we're always hearing things in the past?"

"I suppose so," he said.  "Even if you're really close to something, it still takes some time for the sound to get to you."

Then, an even crazier thought.  "The light takes some time, too, right?  A shorter amount of time, but still some time.  So we're seeing things in the past, too?"

He shrugged.  "I guess so.  Light is always faster than sound."  Then he grinned.  "I guess that's why some people appear bright until you hear them talk."

It was some years later that I recognized the implications of this -- that the farther away something is, the further back into the past we're looking.  The Sun is far enough away that the light from it takes eight minutes and twenty seconds to get here, so you are always seeing the Sun not as it is now, but as it was, eight minutes and twenty seconds ago.  The closest star to us other than the Sun is Proxima Centauri, which is 4.3 light years away -- so here, you're looking at a star as it was 4.3 years ago.  There is, in fact, no way to know what it looks like now -- the Special Theory of Relativity showed that the speed of light is the fastest speed at which information can travel.  Any of the stars you see in the night sky might be exploding right now (not that it's likely, mind you), and not only would we have no way to know, the farther away they are, the longer it would take us to find out about it.

This goes up to some unimaginably huge distances.  Consider quasars, which are peculiar beasts to say the least.  When first discovered in the 1950s, they were such anomalies that they were nicknamed quasi-stellar radio sources mainly because no one knew what the hell they were.  Astrophysicist Hong-Yee Chiu contracted that clumsy appellation to quasar in 1964, and it stuck.

The funny thing about them was on first glance, they just looked like ordinary stars -- points of light.  Not even spectacular ones -- the brightest quasar has a magnitude just under +13, meaning it's not even visible in small telescopes.  But when the astronomers looked at the light coming from them, they found something extraordinary.

The light was wildly red-shifted.  You probably know that red-shift occurs because of the Doppler effect -- just as the sound of a siren from an ambulance moving away from you sounds lower in pitch because the sound waves are stretched out by the ambulance's movement, the light from something moving away from you gets stretched -- and the analog to pitch in sound is frequency in light.  The faster an object is moving away from you, the more its light drops in frequency (moves toward the red end of the spectrum).  And, because of Hubble's law and the expansion of space, the faster an object in deep space is moving away from you, the farther away it is.

So that meant two things: (1) if Hubble's law was being applied correctly, quasars were ridiculously far away (the nearest ones estimated at about a billion light years); and (2) if they really were that far away, they were far and away the most luminous objects in the universe (an average quasar, if placed thirty light years away, would be as bright as the Sun).

But what on earth (or outside of it, actually) could generate that much energy?  And why weren't there any nearby ones?  Whatever process resulted in a quasar evidently stopped happening a billion or more years ago -- otherwise we'd see ones closer to us (and therefore, ones that had occurred more recently; remember, farther away in space, further back in time).

Speculation ran wild, mostly because the luminosities and distances were so enormous that it seemed like there must be some other explanation.  Quasars, some said, were red-shifted not because the light was being stretched not by the expansion of space, but because it was escaping a gravity well -- so maybe they weren't far away, they were simple off-the-scale massive.  Maybe they were the output-end of a stellar wormhole.  Maybe they were some kind of chain reaction of millions of supernovas all at once.

See?  I told you they didn't look that interesting.  [Image licensed under the Creative Commons ESO, Quasar (24.5 mag ;z~4) in MS 1008 Field, CC BY 4.0]

Further observations confirmed the crazy velocities, and found that they were consistent with the expansion of space -- quasars are, in fact, billions of light years away, receding from us at what in Spaceballs would definitely qualify as ludicrous speed, and therefore had a luminosity that was unlike anything else.  But what could be producing such an energy output?

The answer, it seems, is that what we're seeing is the light emitted as gas and dust makes its last suicidal plunge into a galaxy-sized black hole -- as it speeds up, friction heats it up, and it emits light on a scale that boggles the mind.  Take that energy output and drag it out as space expands, and you get the longest-wavelength light there is -- radio waves -- but produced at at a staggering intensity.

All of this comes up because of a series of six papers last week in The Astronomical Journal about a discovery of three quasars that are the most energetic ever discovered (and therefore, the most energetic objects in the known universe).  The most luminous of the three is called SDSS J1042+1646, which brings up the issue of how astrophysicists name the objects they study.  I'm sorry, but "SDSS J1042+1646" just does not capture the gravitas and magnitude of this thing.  There should be a new naming convention that will give the interested layperson an idea of the scale we're talking about here.  I propose renaming it "Abso-fucking-lutely Enormous Glowing Thing, No, Really, You Don't Even Understand How Big It Is."  Although that's a little cumbersome, I maintain that it's better than SDSS J1042+1646.

But I digress.

Anyhow, the energy output of this thing is 5x10^30 gigawatts.  That's five million trillion trillion gigawatts.  By comparison, your average nuclear reactor puts out one gigawatt.  Even all the stars in the Milky Way put together are a hundred times less energetic than this one quasar.

See?  I told you.  Abso-fucking-lutely enormous.

These quasars have also given astrophysicists some insight into why we don't see any close by.  They are blowing radiation -- and debris -- out of the core of the quasar at such high rates that eventually they run out of gas.  The matter loss slows down star formation, and over time a quasar transforms into an ordinary, stable galaxy.

So billions of years ago, the Milky Way was probably a quasar, and to a civilization on a planet a billion light years away, that's what it would look like now.  If you wanted your mind blown further.

The universe is a big place, and we are by comparison really tiny.  Some people don't like that, but for me, it re-emphasizes the fact that our little toils and troubles down here are minor and transitory.  The glory of what's out there will always outshine anything we do -- which is, I think, a good thing.

*******************************

In the midst of a pandemic, it's easy to fall into one of two errors -- to lose focus on the other problems we're facing, and to decide it's all hopeless and give up.  Both are dangerous mistakes.  We have a great many issues to deal with besides stemming the spread and impact of COVID-19, but humanity will weather this and the other hurdles we have ahead.  This is no time for pessimism, much less nihilism.

That's one of the main gists in Yuval Noah Harari's recent book 21 Lessons for the 21st Century.  He takes a good hard look at some of our biggest concerns -- terrorism, climate change, privacy, homelessness/poverty, even the development of artificial intelligence and how that might impact our lives -- and while he's not such a Pollyanna that he proposes instant solutions for any of them, he looks at how each might be managed, both in terms of combatting the problem itself and changing our own posture toward it.

It's a fascinating book, and worth reading to brace us up against the naysayers who would have you believe it's all hopeless.  While I don't think anyone would call Harari's book a panacea, at least it's the start of a discussion we should be having at all levels, not only in our personal lives, but in the highest offices of government.